How is pH calculated when there is no H ion
Contents
How pH is calculated in the Mole Fraction based concentration basis
Overview
The new mole fraction based concentration basis available in the OLI software (ESP version 7.0 or Analyzers 2.0 or later) report activity coefficients on a different basis than in the older software. Hand calculations of such values such as pH can be confusing. This document will take you through two examples of how pH is calculated.
Further confusion is that the reported activity coefficient is different depending on the basis selected. We will examine each basis in turn.
Here is a link to a paper OLI authored on acid-base chemistry in MSE which explains how pH is calculated: MSE Acid-Base Equilibria 2007 (PDF)
Definitions of Symbols and Superscripts
The Standard Aqueous Model
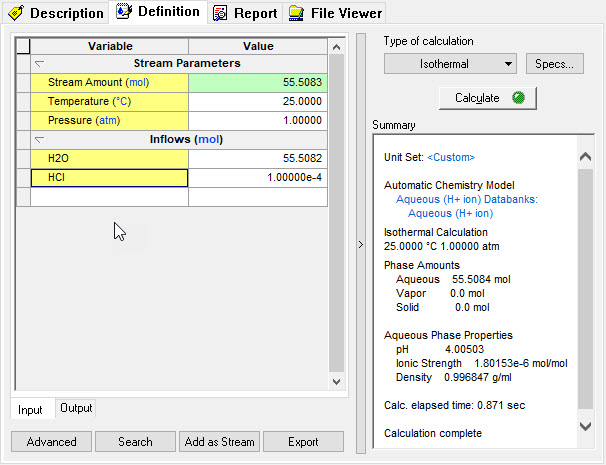
In this simulation we have taken a sample at 25 ⁰C, 1.0 Atmospheres, 55.508 moles of H2O and 0.0001 moles of HCl. The standard Bromley-Zematis activity model was selected.
Input in the software:
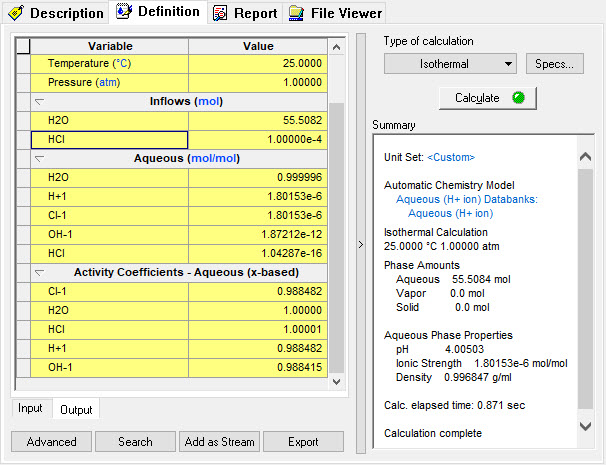
The program reports the following information:
pH definition
Converting to molality based activity coefficients
Calculating the pH on the MSE H+ Basis
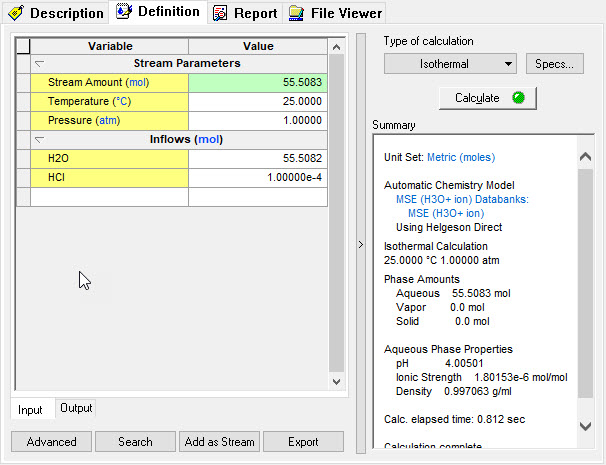
Calculating pH in the hydronium ion (H3O+) basis
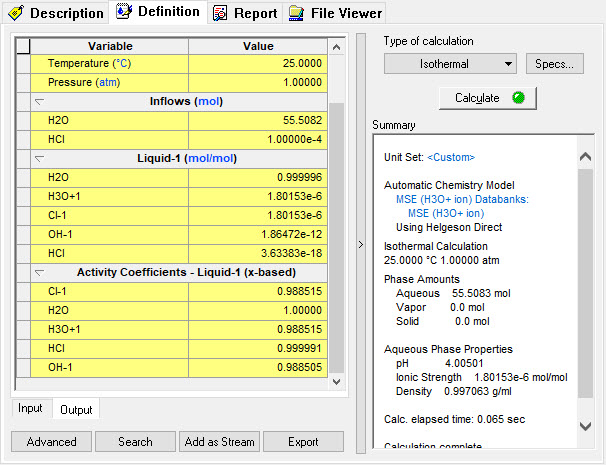
In the hydronium ion basis, there is no hydrogen ion. This makes a direct conversion difficult. Some additional conversions are required. We are using the same compositions as before.
The solution results are:
This was OLI Tip61.