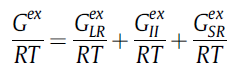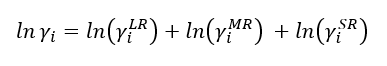Difference between revisions of "Electrolytes and Activity Coefficients"
| Line 20: | Line 20: | ||
[[File:equation2.png|thumb|center|400 px|Equation 2]] | [[File:equation2.png|thumb|center|400 px|Equation 2]] | ||
| − | Where G<sub>LR</sub><sup>ex</sup>, | + | Where G<sub>LR</sub><sup>ex</sup>, G<sub>MR</sub><sup>ex</sup>, G<sub>LR</sub><sup>ex</sup> represent the long, middle and short-range contributions respectively. Thus, the activity coefficient will be given by the following equation: |
| + | |||
| + | [[File:equation3.png|thumb|center|400 px|Equation 3]] | ||
Revision as of 08:45, 24 January 2018
1. How does OLI calculate pH?
To see how the software calculates the pH, please see the following paper on Mo chemistry, Section 3: Solution chemistry of Mo(III) and Mo(IV): Thermodynamic foundation for modeling localized corrosion.
In short, the chemical potential is calculated for each species (base ions, hydrolyzed species, complexes, etc.) according to the following equation:
The chemical potential contains two contributions – the standard contribution (which is directly linked to equilibrium constants) and the activity coefficient from the MSE model. Then, the equilibrium reactions between all species are written and solved according to Equation 1. As always, the key to accuracy is the determination of parameters, which are also described in the paper referenced above.
2. Activity coefficient from MSE model In mixed-solvent electrolytes, the non-ideality of these solutions raises from three different forces:
- Electrostatic forces
- Chemical forces
- Physical dispersion forces
In the MSE the Excess Gibbs Energy is constructed as a sum of these three terms, as follows:
Where GLRex, GMRex, GLRex represent the long, middle and short-range contributions respectively. Thus, the activity coefficient will be given by the following equation: