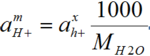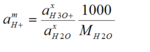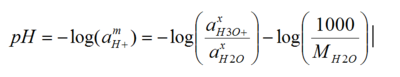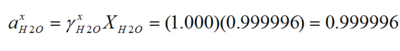Difference between revisions of "How is pH calculated when there is no H ion?"
(→pH definition) |
(→pH definition) |
||
| Line 40: | Line 40: | ||
The definition of pH in the OLI software is the following: | The definition of pH in the OLI software is the following: | ||
| − | [[File: | + | [[File:Image6a]] |
==Converting to molality based activity coefficients== | ==Converting to molality based activity coefficients== | ||
Revision as of 11:05, 8 August 2018
Contents
How pH is calculated in the Mole Fraction based concentration basis
Overview
The new mole fraction based concentration basis available in the OLI software (ESP version 7.0 or Analyzers 2.0 or later) report activity coefficients on a different basis than in the older software. Hand calculations of such values such as pH can be confusing. This document will take you through two examples of how pH is calculated.
Further confusion is that the reported activity coefficient is different depending on the basis selected. We will examine each basis in turn.
Here is a link to a paper OLI authored on acid-base chemistry in MSE which explains how pH is calculated: MSE Acid-Base Equilibria 2007 (PDF)
Definitions of Symbols and Superscripts
The Standard Aqueous Model
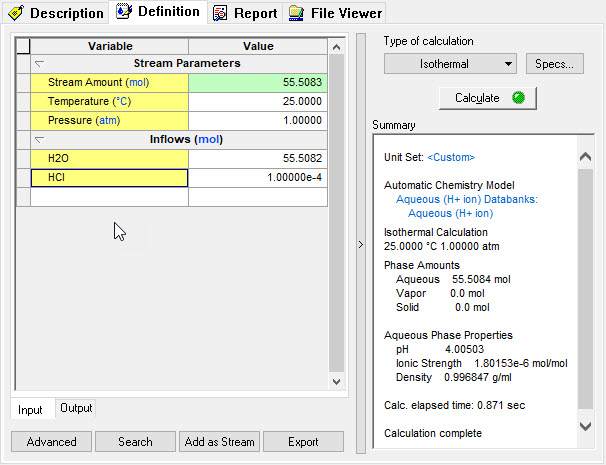
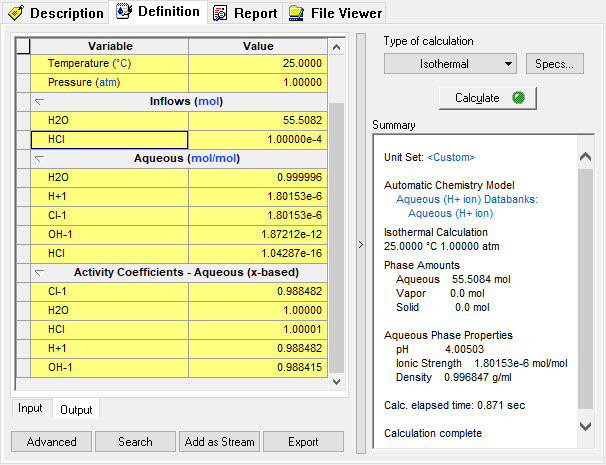
In this simulation we have taken a sample at 25 ⁰C, 1.0 Atmospheres, 55.508 moles of H2O and 0.0001 moles of HCl. The standard Bromley-Zematis activity model was selected.
Input in the software:
The program reports the following information:
pH definition
The definition of pH in the OLI software is the following:
Converting to molality based activity coefficients
To calculate the pH on a molality basis we need to convert the activity coefficient.
The molality concentration unit can be converted easily to the mole fraction basis via this equation: m_(H+)=55.509X_(H+)/X_w
This allows us to define the molal based activity coefficient by expanding both sides of the activity relationship:
a_(H+)^m=a_(H+)^x*(1000/Mw)
γ_(H+)^(m,∞)*55.509* X_(H+)/Xw=γ_(H+)^(x,∞)*X_(H+)*55.509
This solves to:
γ_(H+)^(m,∞)=X_w γ_(H+)^(X,∞)
Evaluating this equation using the simulation values we obtain:
γ_(H+)^(m,∞)=(0.999998)(0.98848)= 0.98848
The definition of pH on the molality basis is:
So you can see that the pH of the solution is the same regardless of the basis.
Calculating the pH on the MSE H+ Basis
The simulation is very similar to previous simulation. Here are the results:
- pH = 4.005
- γHx = 0.988501(activity coefficient for the hydrogen ion – Bromley Basis)
- XH = 1.8 x 10-6 (mole fraction of hydrogen ion)
- XH2O = 0.999998 (mole fraction of water – true basis)
Since the definition of pH is the following: pH=-log(55.509X_(H+)^(x,∞) γ_(H+)^(x,∞) )
We now enter this value in for pH and obtain:
Calculating pH in the hydronium ion basis
In the hydronium ion basis, there is no hydrogen ion. This makes a direct conversion difficult. Some additional conversions are required. We are using the same compositions as before.
The solution results are:
- XH3O+ = 1.8 x 10-6
- XH2O = 0.999996
- γH3O+x1 = 0.988515
- γH2Ox = 1.0000
- pH = 4.005
Our major concern here is that we need to have an effective concentration of the hydrogen ion which does not exist in this framework. We know that the following definition is true:
H3O+ = H+ + H2O
Since the activities on both sides must be equal,
aH3O+ = aH+aH2O
Or
We also know that to convert the mole fraction basis to the molality basis we can use this conversion:
Where MH2O is the molecular weight of water (approximately equal to 18.1054 g/mole)
Thus the activity of the hydrogen ion on a molality basis is:
So pH becomes
Where
And
Thus pH becomes
This was OLI Tip61.