MSE-SRK
MSE-SRK Thermodynamic Model in the OLI Software
Contents
- 1 Frequently Asked Questions (FAQ) about MSE-SRK
- 2 Introduction
- 3 Why was MSE-SRK developed?
- 4 How does MSE-SRK work?
- 5 What are the advantages of MSE-SRK?
- 6 What are the disadvantages of MSE-SRK?
- 7 Summary of Advantages and Disadvantages
- 8 Conclusions
- 9 References
- 10 Species not suitable for MSE-SRK
Frequently Asked Questions (FAQ) about MSE-SRK
Introduction
Starting with version 9.6.1, OLI is introducing a third thermodynamic model in addition to the previously available Aqueous (AQ) and Mixed-Solvent Electrolyte (MSE) models. This new model, called MSE-SRK, is based on the MSE model for electrolyte systems but utilizes the Soave-Redlich-Kwong (SRK) equation of state for both the gas phase and the second liquid (or nonelectrolyte) liquid phase. The MSE-SRK model is targeted at upstream oil and gas and related chemistries and is designed to eliminate the deficiencies that hampered the use of MSE for these applications.
The purpose of this document is to answer the following questions:
- Why was MSE-SRK developed?
- How does it work?
- What are the advantages of MSE-SRK?
- What are its disadvantages?
Why was MSE-SRK developed?
Since 2000, OLI has been intensively developing the MSE thermodynamic framework. Simultaneously, the older AQ model has been maintained and upgraded on an as-needed basis. The MSE model offers major advantages over the AQ model including:
- No limitations with respect to electrolyte concentration, making it possible to simulate electrolyte systems from infinite dilution to pure solute limits;
- Accuracy in predicting the properties of multicomponent systems with multiple competing solid phases;
- Simulating the effects of important organic components (e.g., glycol or methanol) on the behavior of electrolytes;
- Reproducing the properties of systems with two ionic liquid phases;
- Including the computation of solid-gas (or sublimation) equilibria in addition to vapor-liquid, solid-liquid, and liquid-liquid equilibria
Thus, the MSE model represents the state-of-the-art of electrolyte modeling. However, MSE has significant limitations for calculations that include supercritical components at elevated pressures. These limitations are:
- Inability to reproduce the critical behavior of nonelectrolyte mixtures;
- Spurious discontinuities in the phase behavior of systems containing supercritical components at transition points between vapor-liquid and liquid-liquid equilibria arising from the use of different formulations for the gas phase and second liquid phase
Since accurate modeling of systems containing supercritical components at elevated pressures is essential for upstream oil and gas applications, MSE has found limited use in this area. For upstream oil and gas, the AQ model has been generally preferred even though it is clearly inferior to MSE with respect to predicting the behavior of electrolytes. To remedy this situation, the MSE-SRK model has been developed. It retains the state-of-the-art treatment of electrolytes that is a key feature of MSE and, at the same time, introduces the same formulation for the gas phase and second liquid phase to eliminate the above deficiencies of MSE.
How does MSE-SRK work?
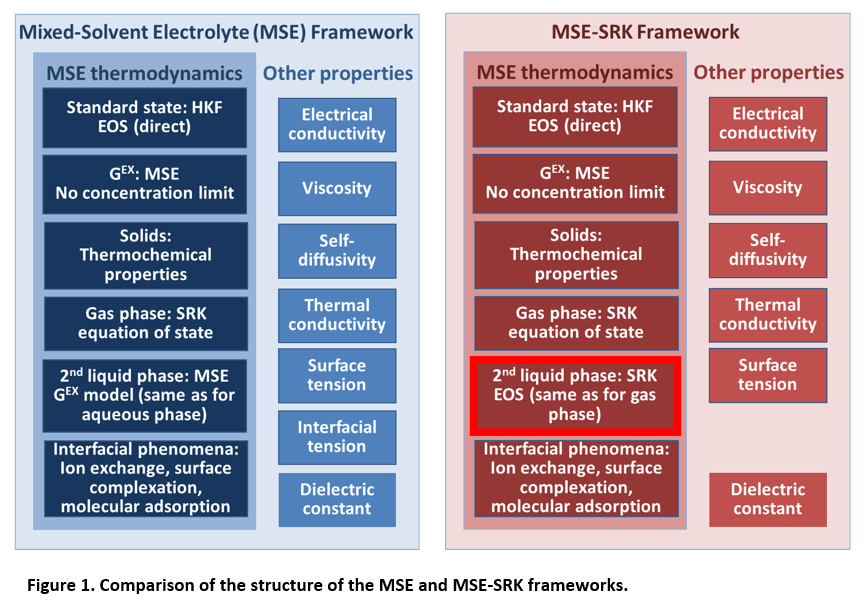
Figure 1 compares the structure of the MSE and MSE-SRK models. The key difference lies in the treatment of the second liquid phase in liquid-liquid equilibrium computations.
In both the MSE and MSE-SRK models, the electrolyte-containing (usually aqueous) liquid phase is represented in the same way, i.e., by a combination of the Helgeson-Kirkham-Flowers (HKF) equation of state for standard-state properties and the MSE activity coefficient model for solution nonideality. Accordingly, the chemical potential of a species i in a liquid phase is calculated as
μiL = μiL,0,x(T,P) + RT ln xiγiX* (T,P,x) (equation 1)
where μiL,0,x(T,P) is the standard-state chemical potential from the HKF theory [1,2], xi is the mole fraction, and γiX* (T,P,x) is the activity coefficient from the MSE theory of Wang et al. [3], which accounts for long-range electrostatic, specific ionic, and short-range intermolecular interactions.
In the case of MSE, eq. (1) is always used for the liquid, whether the system contains one or two liquid phases. This makes it possible to model systems in which both liquid phases are ionic and to predict the transitions from partially miscible to homogeneous liquid systems (i.e., the upper or lower critical solution temperature).
In the case of MSE-SRK, eq. (1) is used for only one liquid phase, i.e., the electrolyte-containing one. The other phase is assumed to be always non-ionic and is modeled using the Soave-Redlich-Kwong (SRK) equation of state [4]. The chemical potential in the non-ionic liquid phase is then calculated as
μiG = μiG,0(T) + RT Ln (P yi φi (T,P) / P0 ) (Equation 2)
where μiG,0(T) is the chemical potential of pure component i in the ideal gas state, yi yi is the mole fraction, φi (T,P) is the fugacity coefficient from the SRK EOS, P is the total pressure, and P0 = 1 atm. The same approach to the second liquid phase is used in the Aqueous (AQ) thermodynamic model (although the treatment of the ionic phase and solid phases is quite different).
For both MSE and MSE-SRK, the properties of the gas phase are obtained from the SRK equation according to eq. (2). Thus, in the case of MSE, vapor-liquid equilibria are always modeled using two separate models – one for the liquid phase and one for the gas phase. This means that MSE can never reproduce the vapor-liquid critical locus. On the other hand, MSE-SRK can easily reproduce vapor-liquid critical behavior for nonelectrolyte systems (e.g., for hydrocarbons and light inorganics). Further, this makes it easy for MSE-SRK to transition smoothly from vapor-liquid behavior to liquid-liquid behavior, which is particularly important when a system contains supercritical components (especially at high pressures).
It is noteworthy that the different treatment of the second liquid phase in the two models leads to a key difference in the representation of critical behavior. MSE can reproduce liquid-liquid, but not vapor-liquid critical end points. For MSE-SRK, the reverse is true, i.e., it can reproduce vapor-liquid, but not liquid-liquid critical behavior.
The properties of solid phases are the same in MSE and MSE-SRK. Thus, when a system contains only a single electrolyte liquid phase and any number of solid phases, MSE and MSE-SRK are equivalent. The transport properties and surface tension are also calculated in the same way in both models (cf. the “Other Properties” columns Fig. 1). The only property that is not available in MSE-SRK is interfacial tension because this property requires a single model for both liquid phases [5].
The difference in the treatment of systems that may form two liquid phases has profound consequences for mixtures containing organics and light inorganic components such as CO2 and H2S. In the rest of this document, we examine these consequences in detail.
What are the advantages of MSE-SRK?
As described above, MSE-SRK uses the same formulation (i.e., the SRK equation of state) for the gas and nonelectrolyte-rich (usually organic-rich) liquid phase. This has two key advantages:
- Any unphysical discontinuities between the vapor-liquid equilibrium (VLE) and liquid-liquid equilibrium (LLE) regions are eliminated
- Vapor-liquid critical behavior is correctly reproduced for hydrocarbon and related systems.
For mixtures that include light components (e.g., light hydrocarbons, CO2, H2S, N2, etc.), a transition between a VLE and an LLE region is predicted as pressure increases at a fixed temperature. The vapor and second-liquid phases can often be classified as supercritical fluids when they are dominated by components such as CH4, CO2 or N2. In such cases, the VLE – LLE transition is smooth and no discontinuities in equilibrium composition are expected. However, it should be kept in mind that such discontinuities may be real for mixtures involving subcritical lighter components (see Springer et al. [6, 7] for a detailed discussion of these phenomena for CO2 and H2S-containing systems).
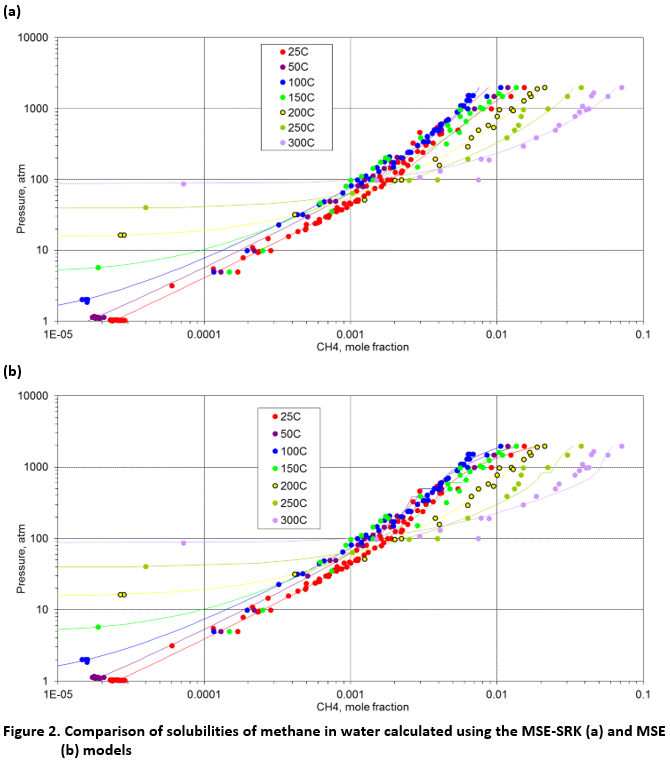
Figure 2 illustrates this behavior for the solubility of methane in water at temperatures ranging from 25 °C up to 300 °C and pressures up to ~2000 atm. Under all conditions shown in Fig. 2, methane is above its critical temperature and, therefore, no discontinuities are evident in the experimental data. The MSE-SRK model (Fig. 2a) reproduces the data with excellent accuracy and with no discontinuities. On the other hand, the MSE model shows some small discontinuities in the calculated solubilities in Fig. 2b. These discontinuities can be seen as short horizontal lines for some isotherms and are associated with the transition from VLE to LLE. It should be noted that the representation of the methane solubility is similar using MSE and MSE-SRK in terms of the overall numerical deviations. Nevertheless, MSE-SRK is superior because it inherently eliminates the discontinuities. It should be noted that both models predict a transition from VLE to LLE and this transition occurs approximately at the extension of the vapor pressure curve of the lighter component. Nevertheless, this transition is completely smooth in the case of MSE-SRK. The MSE and MSE-SRK models show similar behavior for mixtures of water with other light components with or without electrolyte components.
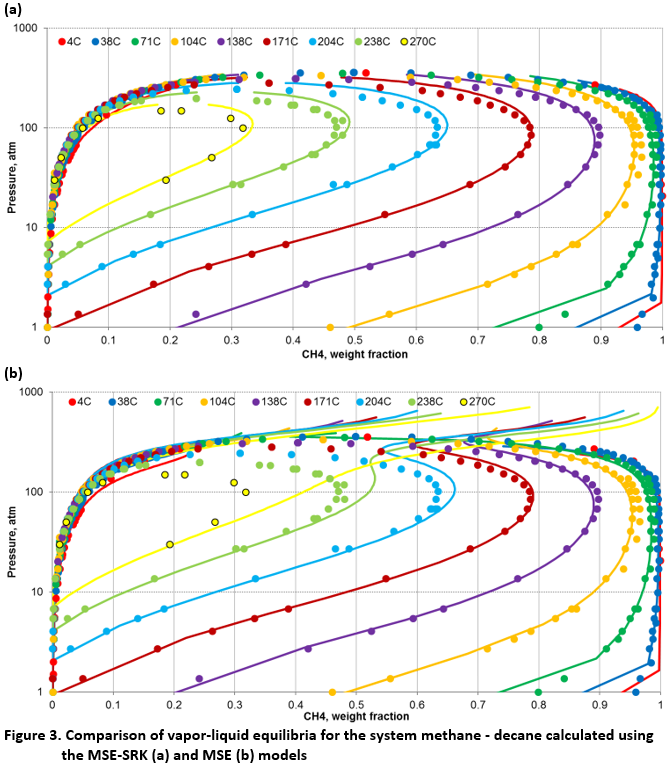
While the differences between MSE and MSE-SRK do not appear to be large for mixtures of water with light components, they become much more dramatic for mixtures of organic components with significantly different volatilities. In such cases, a good representation of the vapor-liquid critical behavior is essential. MSE-SRK can reproduce the VLE critical behavior in such mixtures because the liquid and vapor phases are reproduced using the same equation of state. This is illustrated in Figure 3 for the methane – decane mixture, for which a substantial amount of experimental data is available over a wide range of temperatures. As shown in Fig. 3a, MSE-SRK correctly reproduces the vapor-liquid equilibria. On the other hand, MSE is inherently incapable of predicting the VLE critical behavior. Although MSE correctly represents the bubble- and dew-point curves at lower pressures, far away from the critical point, it does not close the VLE “loops” at higher pressures. Furthermore, it predicts an incorrect extension of the two-phase region at higher pressures beyond the critical locus, where a single phase exists. This extension is an artifact of using separate models for the liquid phase and for the gas phase in hydrocarbon mixtures.
Similar behavior is obtained for other mixtures of nonelectrolytes with strongly different volatilities. In general, MSE-SRK correctly predicts the behavior of such mixtures whereas MSE is correct only when the conditions are not close to the critical locus.
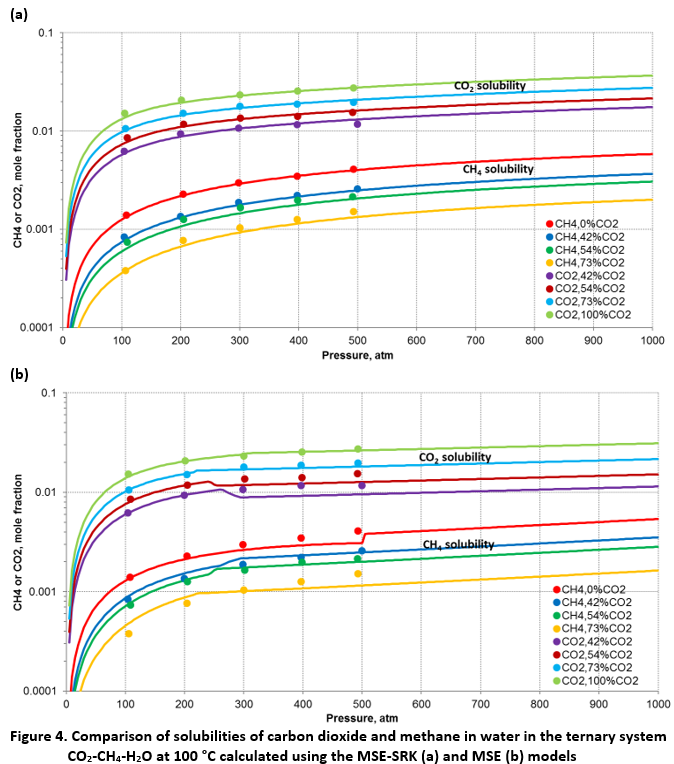
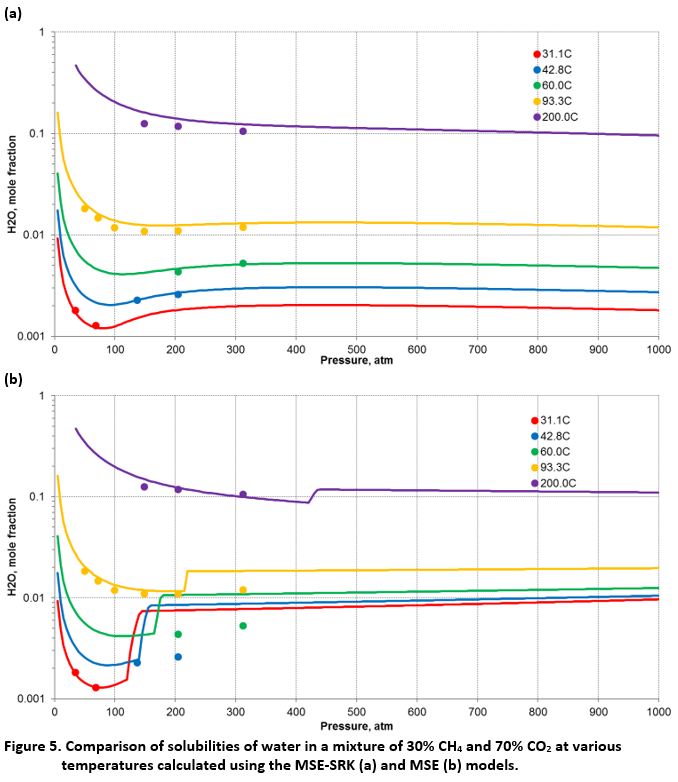
In the case of MSE, the discontinuities between the VLE and LLE regions manifest themselves most clearly for multicomponent systems that contain supercritical components. In multicomponent systems, the discontinuities may be amplified even though they are usually not large in binary water + nonelectrolyte systems as shown in Fig 2b. Figures 4 and 5 compare the MSE and MSE-SRK predictions for a typical system of this kind, i.e., CO2 – CH4 – H2O at pressures up to 1000 atm. The solubilities of CH4 and CO2 in water are shown in Fig. 4 whereas the solubility of water in a CO2 – CH4 mixture is illustrated in Fig. 5.
As shown in Fig. 4b, MSE and MSE-SRK predict essentially the same solubilities of CO2 and CH4 in water in the VLE region, i.e., for pressures up to approximately 200 atm. At higher pressures, MSE shows some discontinuities. Although the discontinuities are not numerically large, they do not reflect physical reality. Substantially larger discontinuities are shown in Fig. 5b for the solubility of water in a CO2/CH4 phase. In the VLE region, the H2O solubilities are also essentially the same. However, the discontinuities in the transition to the LLE region lead to a significant overestimation of the H2O solubility. In all cases, MSE-SRK yields accurate results across the whole range of pressure.
What are the disadvantages of MSE-SRK?
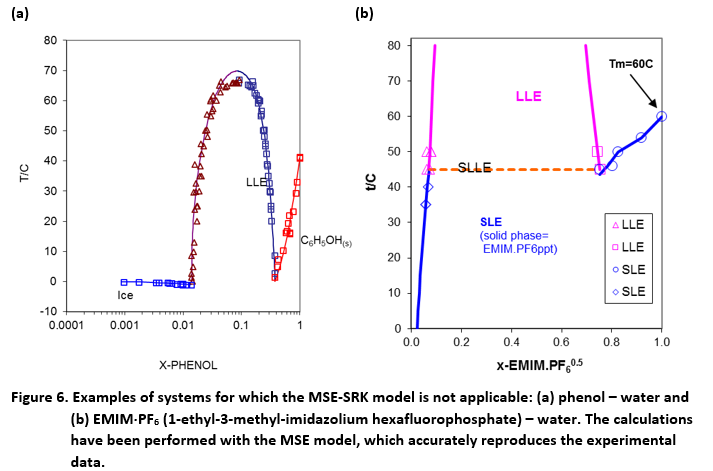
While the use of separate models for reproducing liquid-liquid equilibria (i.e., the MSE activity coefficient model for the electrolyte-containing, water-rich phase and the SRK equation of state for the organic-rich phase) is advantageous for systems containing hydrocarbons and light components, it is not suitable for systems that show liquid phase splitting with upper or lower critical solution temperatures (UCST or LCST). In order to reproduce UCST or LCST, it is essential to use a single model for both liquid phases so that they can merge at UCST or LCST. An example is provided in Figure 6a, which shows the phase behavior of the system phenol – water. This system has an UCST, i.e., liquid-liquid phase splitting occurs only below ~68 °C and the liquid phase is homogeneous above this temperature. This kind of liquid-liquid equilibria is accurately reproduced by MSE as shown in Figure 6a. MSE-SRK is inherently incapable of reproducing such behavior. This limitation is not important for typical mixtures of water, hydrocarbons and light inorganics because the critical end points in such systems occur at temperatures that are not of practical interest. However, this restriction becomes significant for mixtures of various other chemicals.
Further, MSE-SRK cannot reproduce the behavior of systems in which the two coexisting liquid phases contain ions. This is because the SRK equation of state is a non-ionic model. An example of such systems in shown in Figure 6b, which depicts a solid-liquid-liquid equilibrium diagram for a mixture of an ionic liquid (1-ethyl-3-methyl-imidazolium hexafluorophosphate) in water. Although neither UCST nor LCST is important for the system shown in Figure 6b, both liquid phases are clearly ionic and need to be modeled as such. There are other important examples of systems with two coexisting ionic liquid phases, e.g., aqueous solutions of common salts of polyvalent ions (such as phosphates) at high temperatures, aqueous polymer (e.g., polyethylene glycol) – salt mixtures, and mixtures used in thermochemical cycles for hydrogen generation (e.g., HI – I2 – H2SO4 – H2O). Such mixtures can be successfully modeled using MSE.
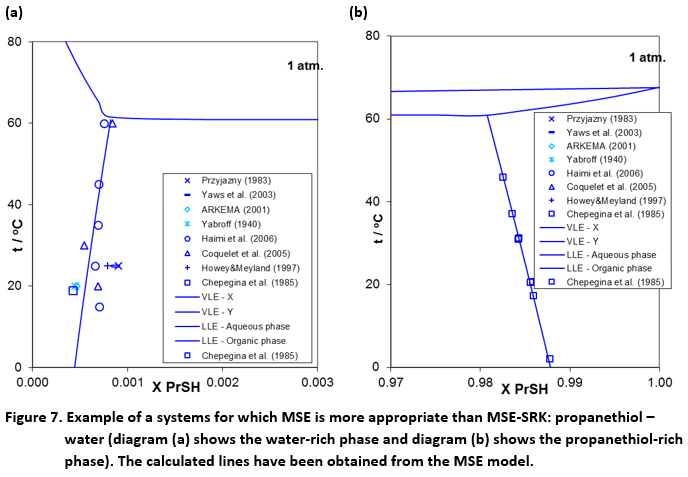
Additionally, there is a class of systems for which MSE-SRK could be used, in principle, with appropriate parameterization but MSE is more accurate. An example of such a system is shown in Figure 7 for the propanethiol (propyl mercaptan) – water mixture. In this case, MSE can very accurately reproduce the compositions of the two coexisting liquid phases whereas the same accuracy is not obtained using MSE-SRK. In general, there is many organic components such as thiols, amines, alkanolamines, disulfides, etc., which have not been designed for use with MSE-SRK. Such components are often encountered in downstream oil and gas applications, in which the pressures of interest are much lower than those associated with upstream environments. At low and moderate pressures, the MSE model does not have the difficulties in the transition from VLE to LLE as described above. Thus, MSE is appropriate for downstream applications.
Because of the above limitations, MSE-SRK is not intended to be used with certain species. A list of these species is provided in the Appendix. If a species from this table is included in the chemistry and MSE-SRK is selected, the OLI software will issue a warning. It is not recommended to proceed with MSE-SRK calculations in such cases unless the components in question are at such low concentrations that they are not likely to affect the overall phase behavior or when it is certain that liquid-liquid phase splitting is not possible in the system of interest.
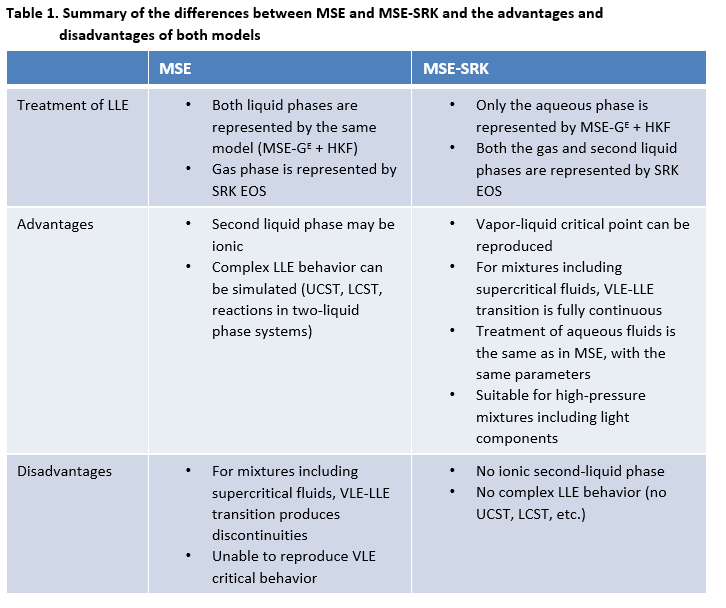
A summary of the advantages and disadvantages of the MSE and MSE-SRK models is given in Table 1.
Summary of Advantages and Disadvantages
Conclusions
- MSE-SRK has been designed primarily for upstream oil and gas systems
- For systems containing only electrolytes in water, MSE-SRK is equivalent to MSE
- MSE-SRK should be selected for systems containing water, salts, hydrocarbons, acid gases and other light components, especially if wide ranges of pressures are considered
- MSE-SRK should not be selected when ionic components are expected in both aqueous and second liquid (nonaqueous or water-depleted) phases, when upper- and/or lower critical solution temperatures occur in liquid-liquid equilibria, and when sublimation (solid-gas) equilibria need to be modeled together with other phase equilibria
References
[1] H.C. Helgeson, D.H. Kirkham, G.C. Flowers, Theoretical Prediction of the Thermodynamic Behavior of Aqueous Electrolytes at High Pressures and Temperatures. IV. Calculation of Activity Coefficients, Osmotic Coefficients, and Apparent Molal and Standard and Relative Partial Molal Properties to 5 kb and 600 °C, American Journal of Science, 281 (1981) 1241-1516.
[2] J.C. Tanger, H.C. Helgeson, Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Revised equations of state for the standard partial molal properties of ions and electrolytes, Am. J. Sci., 288 (1988) 19-98.
[3] P.M. Wang, A. Anderko, R.D. Young, A speciation-based model for mixed-solvent electrolyte systems, Fluid Phase Equilibria, 203 (2002) 141-176.
[4] G. Soave, Equilibrium Constants from a Modified Redlich-Kwong Equation of State, Chem. Eng. Sci., 27 (1972) 1197-1203.
[5] P. Wang, A. Anderko, Modeling Interfacial Tension in Liquid-Liquid Systems Containing Electrolytes, Industrial & Engineering Chemistry Research, 52 (2013) 6822-6840.
[6] R.D. Springer, Z. Wang, A. Anderko, P. Wang, A.R. Felmy, A Thermodynamic Model for Predicting Mineral Reactivity in Supercritical Carbon Dioxide: I. Phase Behavior of Carbon Dioxide – Water – Chloride Salt Systems Across the H2O-Rich to the CO2-Rich Regions, Chem. Geol. , 322-323 (2012) 151-171.
[7] R.D. Springer, P. Wang, A. Anderko, Modeling the properties of H2S - CO2 - salt - water systems in wide ranges of temperature and pressure, SPE Journal, 20 (2015) 1120-1134.
Species not suitable for MSE-SRK
Some species as mentioned above are not suitable for MSE-SRK. Here is a list of those species. All the OLI Software programs will eventually warning the user when such species are in play.