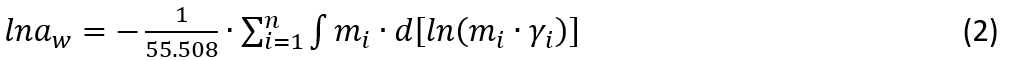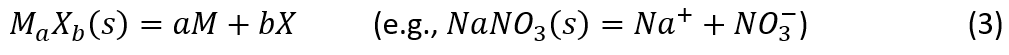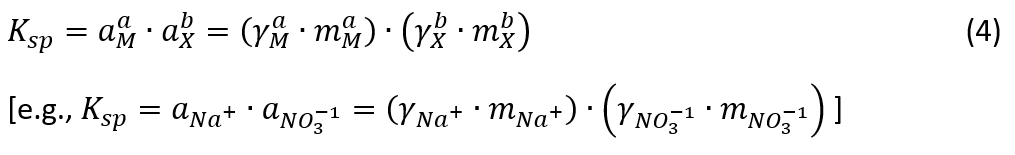Comparing activity coefficients between different thermodynamic frameworks
Question:
I am comparing the activity coefficient of the nitrate ion (NO31-). I looked up the value in OLI Studio for the AQ thermodynamic framework and also in the MSE thermodynamic framework. They differ by over 50% with the MSE derived values being much larger. Why?
Response: From Peiming Wang, PhD. OLI Systems
I agree with the concept that obtaining different activity coefficient values from the two different models (i.e. AQ vs. MSE) under the same total salt concentration, temperature, and pressure conditions if speciation is different (e.g. with or without the ion-pair such as NaNO3(aq) in the NaNO3 solution). This is because activity coefficients are a function of each and all individual species (ions or neutral), and the speciation in the two models are different, resulting in different equilibrium concentrations for individual species, and thus, different activity coefficients.
Below, I am hoping to provide further reasoning on the basis of thermodynamic fundamentals.
Part 1.
In an equilibrium solution at a given temperature and pressure, Gibbs-Duhem equation must hold, i.e.,
where ai is activity of species i: ai=mi∙γi and a0=aw (water activity), and n is the number of species in the solution. Equation (1) can be integrated as (where n0 is set to be 55.508 for 1 kg H2O):
Only binary solution (e.g. NaNO3+H2O) is considered here to simplify the explanation. For an electrolyte that is fully dissociated in the aqueous solution (e.g. NaNO3 in the MSE model), the molality of Na+ and NO3- are the same as the total NaNO3 concentration. If ion-pairing is considered (e.g. NaNO3 in the AQ model), the Na+ and NO3- concentrations will be different from (i.e. smaller than) the total NaNO3 concentration due to the formation of ion-pair, NaNO3(aq). In this case, the molality (m) and activity coefficient (γ) of NaNO3(aq) will also need to be included in Eq. (1) and (2). The value of activity coefficient for each species will be determined based on concentrations of all species present (i.e. Na+ and NO3- in the MSE mode, and Na+, NO3-, NaNO3(aq) in the AQ model, in addition to other less important species such as H+/H3O+ and OH-).
At the same time, for a given solution (i.e. fixed T, P, and total salt concentration), water activity, aw, which is an experimentally measurable property, must be the same (i.e. a value that matches the experimental results under the given condition) regardless of the model (e.g. AQ vs. MSE) used in the calculation.
Part 2
The explanation may be further extended to the solid saturation, i.e. a solution in which solid is in equilibrium with the solution (e.g. at solid-liquid equilibrium). For the solid dissolution reaction:
The equilibrium condition is
For the NaNO3 + H2O system, the concentrations (e.g. molality) of dissociated cation (M=Na+) and anion (X=NO3-) in the MSE model are the same as the total NaNO3 concentration at saturation (as NaNO3 is fully dissociated). These ionic concentrations (e.g. mNa and mNO3), however, are different from (i.e. smaller than) the total NaNO3 concentration at the saturation in the AQ model due to formation of NaNO3(aq) ion-pair:
At the same time, concentrations and activity coefficients of both cation (Na+) and anion (NO3-) must satisfy the equilibrium condition defined by Eq. (4), in which, Ksp is the thermodynamic equilibrium constant that both models should fulfill. Thus, it is impossible for the two models to have the same activity coefficients of NO3- and/or Na+ at the saturated solution due to their different ionic concentrations, which, combined together, must satisfy Eq. (4).
It should be noted, however, it is possible that the equilibrium constant Ksp from the two models may have some (usually small) deviation depending on the data used in parameterizing the model. These parameters include standard-state Gibbs free energy of formation leading to the Ksp values.
Conclusion:
When systems are multicomponent, the variation of the activity coefficients becomes more complicated. In general, it is not surprising that if speciation are different in the two models, the activity coefficient for the same ion can be different under the same inflow conditions at a given T and P.
We emphasize on looking at how well a model predicts measurable properties such as solubility, vapor pressure or boiling temperature, and activity of water. Comparison between the two models against these properties