Modeling SiO2 in MSE v. AQ frameworks
Can you explain why the speciation of the dissociation of SiO2 is significantly different in MSE than in the AQ thermodynamic framework?
OLI has looked into this case and the species under the two models.
The species in the AQ model are:
SiO2(aq)
H3SiO4-1
H2SiO4-2
In MSE the species are:
SiO2(aq)
HSiO3-1
H2SiO4-2
The difference for species between the two models are in the monovalent silicate ions: H3SiO4-1 (in AQ) and HSiO3-1 (in MSE). These two species differ only by one H2O molecule:
H3SiO4-1 = HSiO3-1 + H2O
For modeling acid-base chemistry (and aqueous chemistry in general), we only introduce one of such species based on the information we collected from literature. We have confirmed that these two monovalent species are interchangeable, i.e. ionization constants are identical when one is converted to the other, based on standard-state properties of H2O.
In the MSE modeling, introducing HSiO3-1 is apparently more effective in reproducing large quantity of experimental data on which the model has been developed for the aqueous SiO2 systems (including amorphous and quartz). These experimental data include those for vapor-liquid equilibrium, ionization equilibria, and solubility as a function of temperature (to 350C), pressure (to above 2,000 atm), concentrations of NaOH and salts (e.g. NaCl, KCl, LiCl, CaCl2). In addition, very complex solubility behaviors in the high alkaline system of SiO2 + Na2O + H2O have been very well reproduced based on the selected set of silicate species.
The behavior of speciation with changing pH in the MSE model as shown in the oad case at 85C depends on the ionization equilibrium constants (e.g. standard-state properties) as well as the activity coefficient effects (which also vary with temperature and concentrations). For example, at high pH, the equilibrium between H2SiO4-2 and HSiO3-1 seems to favor the formation of H2SiO4-2 with the increased pH:
H2SiO4-2 = HSiO3-1 + OH-1
It is however also depending on the activity coefficients at the equilibrium, which must satisfy the defined equilibrium condition: Keq = (mHSiO3- . mOH-/mH2SiO4-2).(gHSiO3- . gOH-/gH2SiO4-2) where m is the molal concentration and g is the activity coefficient.
where Keq is the equilibrium constant for the above reaction and g is the activity coefficient of the indicated species. In the MSE model, competition of H2SiO4-2 and HSiO3-1 in the high pH region (based on the above Keq equation) has led to the increased HSiO3-1, rather than H2SiO4-2, at pH above 12. This behavior is not seen in the AQ model because the AQ model has never been calibrated to the full range of conditions from all experimental data used for MSE model calibration, especially at high alkaline conditions, due to AQ model's concentration limit.
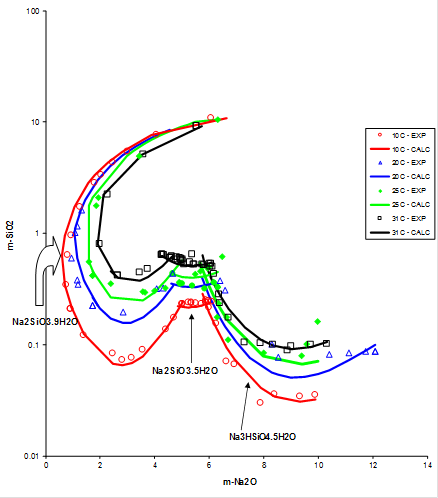
The following plot shows the solubility behavior in the system SiO2 – Na2O – H2O, which has been obtained from MSE:
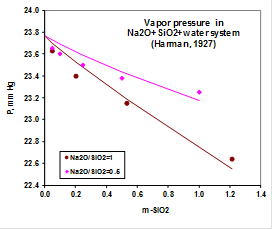
These are solubilities at very alkaline conditions. The AQ model cannot reproduce such complex solubility behavior at all. To reproduce this behavior, it was necessary to model activity coefficients at high alkalinity as described in the analysis above. Also, MSE reproduces the activity of water in the sodium silicate system as shown, for example in this plot:
This indicates that the activity coefficients for silicate species at high alkalinities are reasonably reproduced by MSE.